Skip to content

Deep Learning for Computer Vision

Train Neural Network

One time setup

Activation functions

Sigmoid: \(\sigma(x)=1/(1+e^{-x})\)

  • Squashes numbers to range \([0,1]\)
  • problems:
    • Saturated neurons "kill" the gradients
    • Sigmoid outputs are not zero-centered
    • exp() is a bit compute expensive

Tanh

  • Squashes numbers to range \([-1,1]\)
  • zero centered(nice)
  • still kill gradients when saturated

ReLU: \(f(x)=max(0,x)\)

  • Does not saturate in positive region
  • Very computationally efficient
  • COnverges much faster than sigmoid/tanh in practice
  • Problems:
    • Not zero-centered output
    • When x < 0, the gradient will also be zero, which may cause it never update.

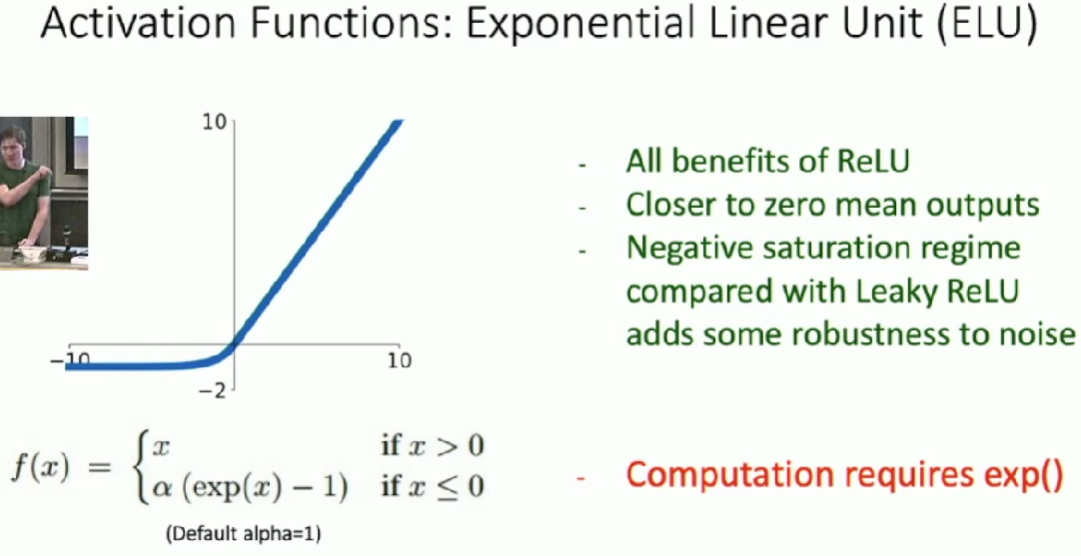
Leaky ReLU: \(f(x)=max(0.01x,x)\)

  • Does not saturate
  • Very computationally efficient
  • COnverges much faster than sigmoid/tanh in practice
  • will not "die" like ReLU
  • We can introduce learnable parameter \(\alpha\), which is call PReLU(Parametric Rectifier): \(f(x)=max(\alpha x,x)\)

Data Preprocessing

  • Subtract the mean image(AlexNet)
  • Subtract per-channel mean(VGGNet)
  • Subtract per-channel mean and divide by per-channel std(ResNet)
  • Others
    • PCA: data has diagonal covariance matrix
    • whitening: covariance matrix is the identity matrix

Weight Initialization

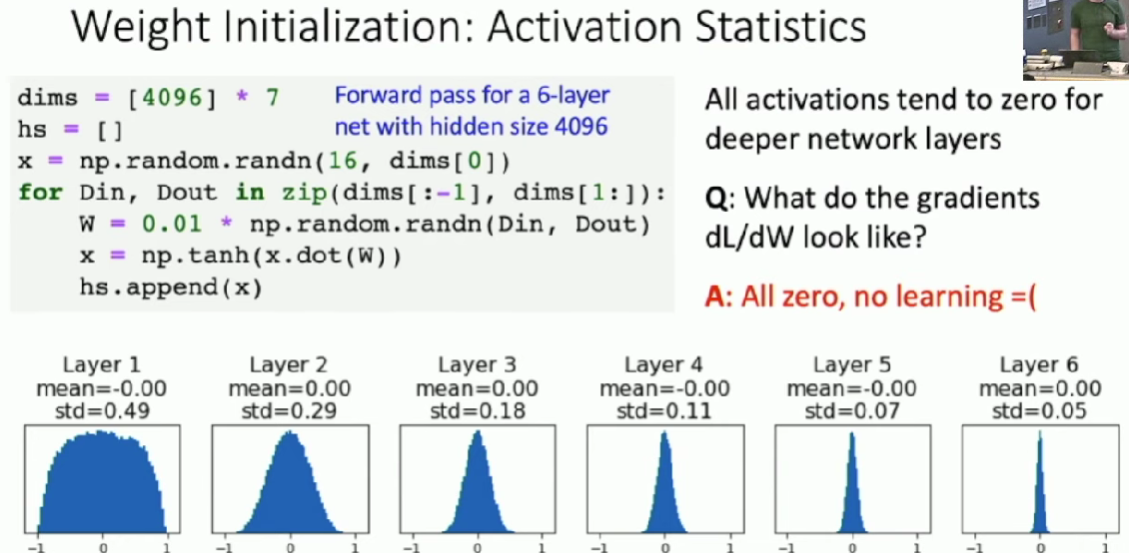
Q: What happens if we initialize all \(W=0, b=0\)?

A: All outputs are zero and weights will never update.

Small random values

Big random values

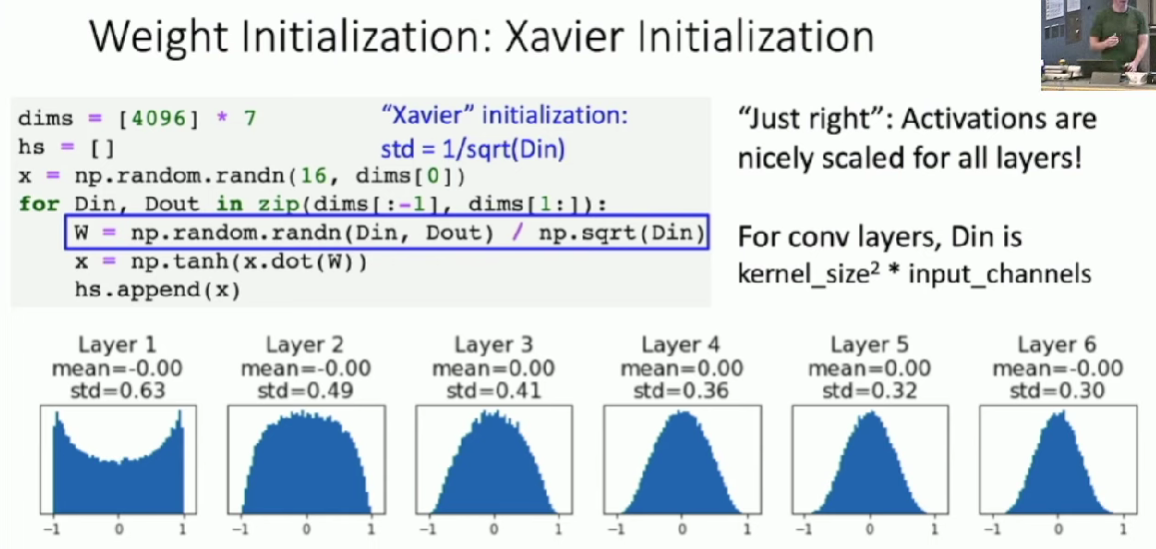
Xavier Initialization

  • Derivation: Varience of output = Variance of input
\[ y=Wx\qquad \qquad \qquad \qquad y_{i}=\sum_{j=1}^{Din}x_{j}w_{j} \\ \begin{align} Var(y_{i})&=Din\times Var(x_{i}w_{i}) \qquad &\text{Assume x, w are iid}\\ &=Din\times (E[x_{i}^{2}]E[w_{i}^{2}]-E[x_{i}]^{2}E[w_{i}]^{2}) \qquad &\text{Assume x, w independent}\\ &=Din\times Var(x_{i})\times Var(w_{i})\qquad &\text{Assume x, w are zero-mean} \\ \end{align} \\ \text{If }Var(w_{i})=1/Din\text{ then }Var(y_{i})=Var(x_{i}) \]

Unfortunately, this initialization tends to be bad when we use ReLU as activation function.

Kaiming / MSRA Initialization * ReLU correction: std = sqrt(2 / Din)

"Just right" - activations nicely scaled for all layers.

Not do well in Residual Networks.

If we initialize with MSRA: then \(Var(F(x))=Var(x)\). But then \(Var(F(x)+x)>Var(x)\) - variance grows with each block!

  • Solution: Initialize first conv with MSRA, initialize second conv to zero. Then \(Var(x+F(x))=Var(x)\)

Regularization

In common use: L2 regularization, L1 regularization ...

Dropout In each forward pass, randomly set some neurons to zero. Probability of dropping is a hyperparameter. 0.5 is common

Forces the network to have a redundant representation. Prevents co-adaptation of features.

Another interpretation: Dropout is training a large ensemble of models (that share parameters). Each binary mask is one model

  • Test Time: We need to take another way to compute output when testing or our output will be random.
    • We want to "average out" the randomness at test-time. That is, multiply the result without dropout by dropout probobility.

Inverted Dropout Drop and scale layer during training,

Data Augmentation

Tranform input training image before feeding it into the network. Horizontal flips is one example. This augments the amount of data and keep their label unchanged.

Random Crops and Scales

  • Training: sample random crops / scales

    • Pick random L in range [256, 480]
    • Resize training image, short side = L
    • Sample random 224 x 224 patch

  • Testing: average a fixed set of crops

    • Resize image at 5 scales: {224, 256, 384, 480, 640}
    • For each size, use 10 224 x 224 crops: 4 corners + center, + flips

Training Dynamics

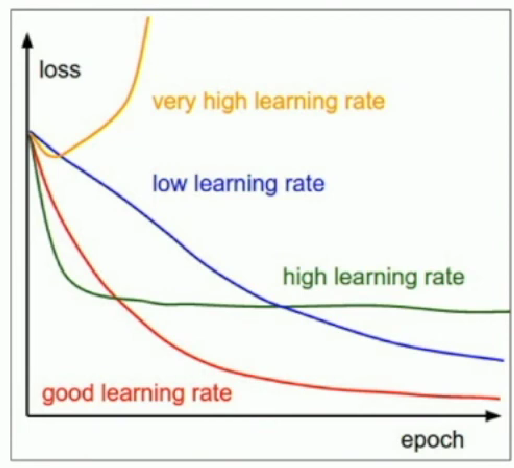
Learning rate schedules

We can Start with large learning rate and decay over time.

Step Schedule

Step: Reduce learning rate at a few fixed points.

E.g. for ResNets, multiply LR by 0.1 after epochs 30, 60, and 90.

  • Problem: introduce additional hyperparameters we have to tune.

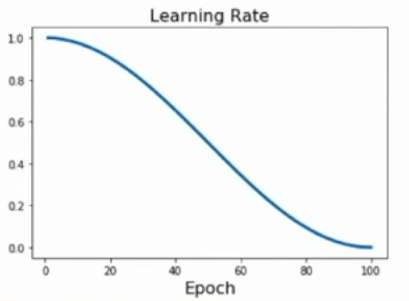
Cosine Schedule: \(\alpha_{t}=\frac{1}{2}\alpha_{0}(1+cos(t\pi /T))\)

Linear Schedule: \(\alpha_{t}=\alpha_{0}(1-t/T)\)

Inverse Sqrt: \(\alpha_{t}=\alpha_{0}/\sqrt{t}\)

Constant: \(\alpha_{t}=\alpha_{0}\)

  • Early Stopping: Stop training the model when accuracy on the validation set decreases. Or train for a long time, but always keep track of the model snapshot that worked best on val. Always a good idea to do this!

hyperparameter optimization

Grid Search

Choose several values for each hyperparameter(Often space choices log-linearly).

Example:

Weight decay: [1x10-4, 1x10-3, 1x10-2, 1x10-1], Learning rate: [1x10-4, 1x10-3, 1x10-2, 1x10-1]

Evaluate all possible choices on this hyperparameter grid.

Random Search

Randomly choose several values for each hyperparameter in a given range(Often space choices log-linearly)

Example:

Weight decay: log-uniform on [1x10-4, 1x10-1], Learning rate: log-uniform on [1x10-4, 1x10-1]

  • Jump out of the grid and may have a better performance when some parameters are not important.

Choosing hyperparameters:

Step 1: Check initial loss

Turn off weight decay, sanity check loss at initialization

Step 2: Overfit a small sample

Try to train to 100% training accuracy on a small sample of training data (~5-10 minibatches); fiddle with architecture, learning rate, weight initialization. Turn off regularization.

Loss not going down? LR too low, bad initialization

Loss explodes to Inf or NaN? LR too high, bad initialization

Step 3: Find LR that makes loss go down

Use the architecture from the previous step, use all training data, turn on small weight decay, find a learning rate that makes the loss drop significantly within ~100 iterations

Step 4: Coarse grid, train for ~1-5 epochs

Step 5: Refine grid, train longer

Step 6: Look at loss curves

Step 7: GOTO step 5

After training

Model ensembles

  1. Train multiple independent models

  2. At test time average their results

Transfer learning

  1. Train on Imagenet

  2. Use CNN as a feature extractor. Remove those fully connected layers in the last and freeze other layers.

  3. Bigger dataset: Fine-Tuning

Reinitialize those last layer to new layers and continue training CNN for new task.

Some tricks:

  • Train with feature extraction first before fine-tuning

  • Lower the learning rate: use ~1/10 of LR used in original training

  • Sometimes freeze lower layers to save computation

Large-batch training

How to scale up on data-parallel training on K GPUs?

Goal: Train for same number of epochs, but use larger minibatches. We want model to train K times faster

Single-GPU model: batch size N, learning rate \(\alpha\)

K-GPU model: batch size KN, learning rate \(K\alpha\)